La page ludomathique d'Accrodemaths.

Chaque mois des problèmes sympas sur un thème particulier
Continuons notre voyage dans la capitale anglaise.
(solutions)

Ces jeux ont été lus fois



Solutions :

Royal Festival Hall :
Il y a 5! ordres possibles pour les 5 grands orchestres soit 120.
Le nombre de programmes qui soit tel qu'aucun des cinq orchestres ne se produise le jour prévu, peut être établi par l'arbre suivant :

Il y a 4x11=44 extémités à cet arbre correspondant aux 44 programmes totalement prévus.
D'où la probabilité correspondante : 44/120.

Victoria, waterloo et les autres ... :
Soit n, ce nombre inconnu de gares.
Probabilité que tous leurs noms commencent par des lettres différentes :
Pn = 25/26 x 24/26 ...[26-(n+1)]/26
D'où P6=0,5366, P7=0,4128.
Il y a donc sept gares principales à Londres :
Victoria, Paddington, Waterloo, King's croos, Euston, London bridge et Liverpool street.
Elles ne commencent pas toutes par des initiales différentes, ce qui correspond donc à une probabilité supérieur à 1/2.

Kensington's Garden :
Les huit quarantième des poissons sont marqués, alors que j'en ai marqué quarante.
Le nombre total de poissons de Round Pond est donc approximativement de
40x40/8=20

House of Parliament :
Le nombre de présents parmi les Conservateurs et les Travaillistes est égale au nombre total des Conservateurs : 338.
Le nombre de présents parmi les Autonomistes et les Unionistes irlandais est égale au nombre total d'Unionistes : 10.
Le nombre de présentsparmi les Sociaux-Démocrates et les Libéraux est égale au nombre total de SD : 14
D'où la prportion de présents : 362/634, soit 57,1%.

De tower Bridge au British Museum :
Prenons comme unités les km, h et km/h.
Soit 2x cette longueur inconnue.
Temps de trajet aller : x/5 + x/4 = 27x/60
Temps de trajet aller-retour : 2x/30
Temps total de visite : 1h52min+45min=2h37min
Temps total de trajet : 12h22min-8h12min-2h37min=1h33min (1,55h)
D'où l'équation : (27x+4x)/60=1,55 et donc x=3km.
Il y a donc 6km entre la tour de Londres et le British Museum.

Trafalgar Square :
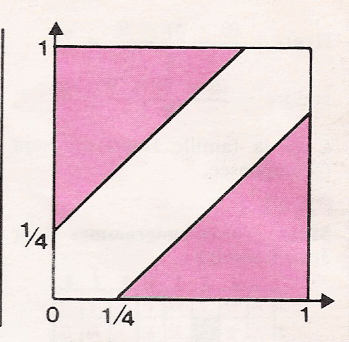
Considérons 2 axes orthonormés. L'heure d'arrivée de Tom est indiquée en abcisse et la mienne en ordonnée.
L'origine correspondant à 9h00 pour chaque axe.
Chacun des points du carré1x1 correspond à une probalité équiprobable.
Sachant que Tom est arrivé à une heure donnée, il me rencontrera à condition que je sois arrivé dans le quart d'heure précédent, ou bien que je me disposai à arriver dans le quart d'heure suivant.
La probabilité que nous ne nous rencotrions pas correspond à l'aire"rosée", c'est à dire à la surface d'un carré de côté 3/4 donc 9/16 :

Haut de page