La page ludomathique d'Accrodemaths.

Chaque mois des problèmes sympas sur un thème particulier
Une première escale en Norvège Brrrrrr...
(solutions)

Ces jeux ont été lus fois



Solutions :

Bergen :
Prenons comme unités les m, min et m/min.
Soit x la dénivellation.
Temps de trajet en funiculaire : 2x/30 = x/15.
Temps de montée et descente à pied : x/5 + x/15 = 11x/60.
C'est le temps à passer en haut, si l'on ne prend pas le funiculaire.
Temps total de la promenade : 130min.
D'où 130 = x/4 + 11x/60 Soit x = 300.
Floyen est à environ 320m d'altitude.

Alesund :

Modle :
Soit n, ce nombre inconnu supposé inférieur à 1000.
Si n est supérieur ou égal à 100, on a n = c d u ; et : (100c + 10d + u) - (100u + 10d + c) = 9; ou 99(c - u) = 9.
Impossible car c et u sont entiers. Donc n<100.
Soit n = 10d + u, on a (10d + u) - (10u + d) = 9; ou d = u + 1
d'autre part : d² + u² = 113 d'où u² + ( u + 1)² = 113
Donc u = 7 et d = 8.
Il y a donc 87 sommets enneigés qui dominnent le fjord de Modle.

Trondheim :
En écrivant deux fois consécutivement un nombre à trois chiffres c d u, on a :
cducdu = (100c + 10d + u)(1001) = (100c + 10d + u)(7 x 13 x 11).
Les divisions succéssives par 7, 11 et 13 (qui donnent toutes des restes nuls) vont refaire apparaître le nombre primitif.
Apparemment, ce n'est pas un miracle de Saint Olav Tryqqvesson

Namos :
Nous pouvons assimiler cette nappe de pétrole à un trapèze isocèle avec pour côté les 6ème et 7ème méridien
pour petite base le 66ème // et grande base le 65ème //.
La grande base fait 40 000 x cos66/360
La petite base fait 40 000 x cos65/360
La hauteur fait40 000/360
La surface en km² est donc de : 40 000/360 x (40 000/360)(cos65 + cos66)/2
Soit 5 123,456 km²

Le Lofoten :
Dans l'ïle de Moskensoy, on ne peut évidement trouver plud de trois routes.
.

Dans l'ïle Austvagoy, on ne peut trouver plus de 9 routes.


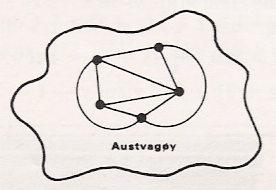
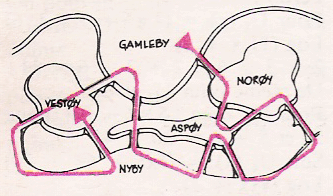
Dans l'île de Vestvogoy, il y a au maximum quinze routes.
En effet, à partir du graphe à 3 sommets, chaque nouveau sommet sera dans une face triangulaire si le précédent est saturé et ne donnera donc que trois nouvelles routes :


N = 3(n - 2) avec n le nombre de village, et N le nombre maxi de routes directes sans croisements.
Sur les trois îles Lofoten, il ne peut y avoir plus de 27 routes.

Nordkapp :
On peut réaliser le tableau ci-dessous :

Avec 11, la cinquantaine est dépassée.
D'où, il n'y avait que 45 pingouins au départ.
Les 38 restants du vol se sont scindés en triangle à 4 rangs (10) et un à 7 rangs (28)

Kirkenes :
Si le départ est à 23 heuers, le premier bateau en sens inverse à 11 heures du matin le lendemain, le suivant douze heures plus tard, etc. en cinq jours et six nuits, la petite aiguille sera passé dix fois sur le 11.
J'ai donc entendu dix fois le sirène durant la montée vers le nord, dix fois aussi pendant la descente vers le sud.
Ce qui fait en tout 20 coups de sirène.

Haut de page